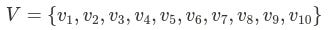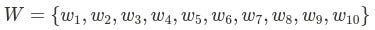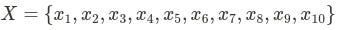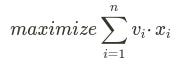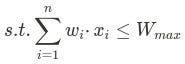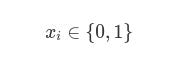📈 #27 (Microsoft's) Knapsack Problem
Will this smart backpack solve the knapsack optimization problem?
The other day I was reading a news article about Microsoft's new smart backpack1.
Yes, they've already patented it, just in case.
The truth is that it's amazing: it integrates Artificial Intelligence, can identify objects around you, access information, and even interact with other devices. And to do this, it uses a camera, microphone, speaker, and processor to analyze its surroundings and respond to your voice commands 👏🏻
But when I go traveling, what I want to know is how to pack my clothes in it without leaving anything important behind. Mind you, it's not a trivial problem; I need to understand the benefit of packing each pair of pants, shirt, and sweatshirt, knowing that it will take up space where no other garment can fit.
Will Microsoft's new smart backpack be able to solve this problem?
I don't know, but what I do know is that it's a very interesting optimization problem, and in this edition of Factibles I tell you about:
What this problem is
Its computational complexity
An example of solving it on Google Sheets
Its real-life applications and problem variants
Let's go for it!
Do you remember when I told you about my trip to Vietnam and how we organized the trip?
What I didn't tell you at the time is that I only carried a backpack with everything necessary: clothes for a week (even though I was there for two), personal hygiene accessories, and the usual mobile charger, Kindle, tablet…
But I wasn't quite sure what weather I would encounter. It was August, so it was definitely going to be hot, but in the rice terraces of Sa Pa, which are in the north of the country and in a very mountainous area, there's a lot of humidity and it could get cold at night. So, I wasn't very clear on what to pack. Mostly summer clothes, even a swimsuit in case we went to the pool or the beach (which we did), but also some light warm clothing.
I'm sure you've experienced something similar.
The problem is that you're not quite sure what to pack. If you include a pair of long pants, a couple of sweatshirts for those cold days, and a light jacket with a hood in case it rains, it weighs more and takes up a lot of space in the backpack, forcing you to reduce the summer clothes, depriving you of the chance to wear those shorts you just bought. You have to balance the situation and make a decision.
And I don't know about you, but I see this as an optimization problem, right? On one hand, you have the backpack, a limited space with a maximum weight you can carry, and on the other, you have the clothes you want to pack with the goal of enjoying your trip to the fullest. Welcome then to…
🎒 The Knapsack Problem
I'm going to name everything we've seen so far, although the problem is practically defined already.
First step: informal definition
On one hand, we have the items we want to put in the backpack. Each item has a value and a weight that will help us decide which items to put in the backpack.
On the other hand, we have the decision we need to make: which items to put in the backpack. From a more formal point of view, we can see it as a binary decision variable for each item with which we establish whether we want to put that item in the backpack (1) or not (0).
We also have to consider the maximum weight of the backpack, which will limit us when choosing the items. This will be the main restriction of the problem.
Finally, the definition of the objective, which is to maximize the total value of the backpack, meaning that the sum of the values of the items we finally put in the backpack is as high as possible.
Second step: translation into mathematical elements
Going a step further, we can define the items as a vector or an array of n elements. Moreover, since for each item we have:
Weight
Value
Decision on whether it goes into the backpack or not
We can create 3 different arrays of n elements that define these 3 different properties. Imagine we have 10 items:
For value:
For weight:
For the decision variable:
Thus, if we want to refer to the value, weight, and decision variable of any given item, we access it through an index i. For example, the value, weight, and decision variable associated with item 3 would be, respectively, V3, W3, and X3.
Additionally, we have a basic parameter for the main restriction: the maximum weight. We can define it as Wmax.
Third step: formal mathematical definition
Well, let's put it in mathematical format, shall we?
First, the Objective Function must capture the definition of what we want to maximize. In this case, the total value of the backpack. We achieve this by multiplying each decision variable by the value of the respective item, and summing all of it:
We have to take into account that the backpack cannot exceed a defined maximum weight, Wmax. The same concept as with the Objective Function, but applied to the weight:
Finally, a very important detail is defining what the decision variables are like. As I told you before, for this problem we choose binary variables:
And with this, we would be ready to solve the knapsack problem… Or not?
🖥️ Computational Complexity
Let's do an exercise together. Let's see if we can manually solve a knapsack problem in which we have 10 items with:
What I'm going to do is: open a Google Sheets and create a column for the values of the items and another for the weights. Then, a column for the decision variables, which I'll manually modify to put a 1 or a 0 in case I want to (or not) include the item in the backpack. I'll also put in another cell the maximum weight of the backpack. Finally, there will be 2 other cells that calculate the value and weight of the solution, respectively, by multiplying the value and weight by the decision variables.
I'm not just saying it, I'm doing it:
As you can see, we could spend a long time trying different options, adding and removing items from the backpack. There are only 10 items, but solving the problem is not trivial. I invite you to do an exercise like this, and add more items if you want. You'll see that with each new item you add, the complexity of solving the problem increases significantly.
I'll tell you in advance: for small examples (like the one we just saw on Google Sheets) it can be optimally solved in very little time, but for sufficiently large examples of this problem there is no efficient algorithm that solves it, that is, there is no algorithm that gives you the optimal solution in a very short period of time.
If you want to delve into what types of algorithms help you solve this problem, the Wikipedia page has several examples of it. You can see dynamic programming algorithms, greedy algorithms... Even algorithms for quantum computers!
I said that for this example we saw it could be solved optimally in a short time, right? Well, again, I'm not just saying it, I'm doing it:
What you just saw is how it is automatically solved with OpenSolver, a tool that allows you to mathematically model an optimization problem and solve it. It's true that not all problems can be solved, and it's a bit limited in terms of the size of the problem, but it still serves to see how a problem of this type could be solved on a small scale.
🌍 Real-world Applications
I'll be honest, in real-life business, people don't talk about the knapsack problem. Each business has its own problem and treats it as such. Moreover, the definition might not exactly fit what I just told you, so often people talk about their own variants of the problem. Let's see some examples of all this:
Investment portfolio optimization.
In an investment portfolio, you have a set of assets to invest in with a maximum budget, and what you would like is to maximize the return on investment. There are many related concepts here because what is the return on investment? How do you calculate it? There are certain statistical techniques and Machine Learning methods that try to predict this value.
Assuming we know this value, we would already have what we also called value in the knapsack problem. The weight would be the risk associated with the asset, and this risk is usually associated with the asset's volatility, which in statistical terms is usually equivalent to the standard deviation of the investment return.
The capacity of the backpack here would correspond to the maximum budget you have for investing, and the decision variables would represent whether we include or exclude each of the assets we have in the investment portfolio. All this with the goal of maximizing the return on investment.
Cutting stock problem in factories.
In this problem, we have a factory that produces goods with a series of materials, and we need to cut those materials into pieces with specific patterns to make those products. For example, we could talk about fabrics with specific patterns to make T-shirts: in the factory, we would have a very, very long piece of fabric and we would have to cut it in such a way that we maximize the number of T-shirts we can make with it, or minimize fabric waste.
So, on one hand, we have the backpack, which would be that long fabric from which we are going to make T-shirts. On the other hand, we have the cost of the solution associated with the waste generated, that is, how much fabric will be left unused for making the T-shirts. Another aspect would be the actual value of the T-shirts made, which could be measured by the demand for that T-shirt. And finally, as a decision variable, it could be how many T-shirts of each type we want to make.
As you can see, I've already introduced a change from the original problem. In the original problem, we had binary decision variables that represent whether an item is in the backpack or not. However, here I mentioned it could be an integer number that represents how many items of each type we are going to make.
Some typical variants of the problem.
The bounded/unbounded knapsack problem is a variant of the problem that removes the restriction that only one item of each type can be chosen, allowing for multiple selections. Exactly what we've just seen now. Whether it's bounded or not tells us if we have a limit on the number of items of each type (for example, we cannot make more than 5 T-shirts with design A nor more than 7 T-shirts with design B), or there is no limit at all.
There's also the quadratic knapsack problem variant, in which we have either a quadratic objective function or quadratic-type restrictions. This means there's a quadratic relationship between decision variables, which can occur, for example, in the investment portfolio optimization problem when we assume certain correlations that can occur between pairs of assets, benefiting or harming the overall set of assets in the solution.
🏁 Final Conclusions
I especially like the knapsack problem: it's very easy to understand and yet has very powerful applications in the industry.
That's why I wanted to present it to you here today, telling you:
Despite its simplicity, it's complicated to solve.
There are algorithms that provide good solutions in a short time.
You could solve it in Google Sheets, modeling the problem with OpenSolver.
Its principles help us make efficient decisions with limited resources in real life.
For all these reasons, when you're packing your suitcase for your next trip... Remember that there are optimization algorithms that could help you!
In any case, if you're already using this framework, what problems are you using it for and how are you doing it? I love seeing new applications to the typical optimization problems.
See you soon,
Borja.
PS: yes, the post title is a play on words. On one hand, it alludes to the typical knapsack optimization problem; on the other, it links to the backpack patented by Microsoft; and finally, to the problem Microsoft has in not being able to solve the knapsack problem with its new backpack.