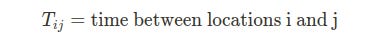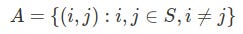📈 #10 Optimizing wanderlust: turning a Vietnam adventure into a data-driven exploration
The math behind planning the perfect trip.
Have you ever been so overwhelmed by travel planning that you felt like your head was going to explode?
I know I have.
I'm a big fan of travel, but I'm also a bit of a control freak. I like to plan everything out in advance, and I hate surprises.
So when it comes to travel planning, I spend hours and hours researching different destinations, itineraries, and transportation options.
But there is a way to make travel planning easier and more efficient. And you know it before I tell you so: optimization.
In today’s post, I'm going to share a bit about how to use optimization for travel planning. But you know what? It was pretty hard at the beginning.
Let’s go for it!
Last summer my wife -girlfriend at that time- and I were planning to go to Vietnam. We wanted to spend 2 weeks there, so we needed to choose the places to visit. You know, the typical googling around what places to visit, some YouTube videos and so on. So we ended up with a list of places to visit.
But then we needed to decide the order of the visits.
This task was not so easy, in Vietnam there are countless options available for you to do: you can enter Vietnam from the north and exit from the south, or vice versa. You can use Hanoi as a base for your travels in the north, or you can move to each region with all your luggage. You can take a night bus to Sapa and spend just one night there, or you can spend several nights and go by day bus. You can take a night train from Ninh Binh to Dong Hoi to visit Phong Nha-Ke Bang National Park the next day, or you can invest that time in flying from Hanoi to Da Nang to reach Hoi An earlier.
Making a decision was hard, and when we finally finished the plan… Then more places to visit appeared! So we needed to replan some parts of the trip, repeating the process until we got to a better solution. And this could become a repetitive task not only for this trip but also for the nexts to come, so…
🤔 How do you choose the best itinerary for your trip automatically?
The problem is all about planning: making decisions given some constraints to get to a goal. The thing is that everything we knew at that time was very vague to come up with a mathematical expression. How could we translate “maximize the total happiness we get from the trip” or “visit the best places without spending too much time in transportation” into maths?
Up to this point, we wanted to define the problem as simple as possible, capturing the ideas we had in plain terms. We already had a budget, a time constraint, and we came up to removing a lot of things until we got our real objective.
Minimizing time traveling.
And this is where optimization comes in. There exists one problem pretty similar to this one: the Traveling Salesman Problem, or the TSP for short. It is a typical one when starting on Operations Research, and it applies to many problems related to logistics or manufacture of microchips, among others.
The TSP needs a graph as a data structure (we used it in another problem too, remembrer?), where nodes represent locations to visit and edges the relationships among them. In this case, the relationships represent distances, or time, or costs to go from one location to another one.
Going back to our problem, since distance means nothing when you can choose between different types of transportation (bus, train, taxi, plane), here I did a time matrix to represent the time it takes to go from one place to another (assuming we were going to take the best possible transportation system beetween locations).
In the picture above I don’t have all possible combinations between locations, but constructing them is trivial: going from Ha Long Bay to Ninh Binh includes passing through Hanoi so it will take 2h 30 min from Ha Long Bay to Hanoi + 2h from Hanoi to Ninh Binh, and so on and so forth. Ah! And another thing we discarded: the 3h flight from Hanoi to Da Nang since it is clearly not a good idea if you want to visit Ninh Binh and Phong Nha-Ke Bang National Park (which I strongly recommend). For those impossible connections we can set an infinit value in the matrix.
Finally the time matrix will look like this (simplifying it to only have integer numbers):
Take a look at that table: it’s almost symmetric. Almost. Going from Da Nang to Hanoi takes only 3 hours since you can go back by plane without visiting any other location.
What did I do the next?
💡 Building a mathematical model
Now that I know the data (locations to visit and the time it takes to go from location to location), I need to decide in which order to visit the locations in a way that I minimize the total time of traveling such that all locations are visited just once starting and finishing from Hanoi.
Look that I wrote everything we need for a mathematical model: data, decision variables, objective function and constraints. How to model everything?
Data
For the data we need to define sets and parameters, as they are the mathematical blocks to build the list of locations and the time matrix we described above.
The list of locations to visit then is
while the time matrix between any pair of locations is
Set of possible arcs:
Decision variables
Here I would write a definition for the actions I want to take: what is the order for visiting all the locations? I would like the model to answer that question for me, so those are the decision variables. Something like the potential actions to take. In this case, I want to know if I go from one location to another, and in that case the model should set a 1 (or True), 0 (or False) otherwise:
Constraints
We need to translate the following sentences into mathematical terms:
All locations are visited.
Each location is visited once.
The last location visited is the location we started from (making a closed tour).
But if you think it carefully, you will see that the second sentence includes the other two: if each location is visited once it means that all locations are visited… And if we get a closed tour from the solution, it’s because we visited each location once.
In the end it translates into entering and exiting nodes must be one for each node, so it’s a pair of constraints:
For each location i, the sum of the decision variables indicating the entrance to that location must be equal to 1.
For each location i, the sum of the decision variables indicating the exit from that location must be equal to 1.
These constraints ensure that each location is visited once and that the tour is closed, meaning the last location visited is the same as the one we started from.
The thing is, if you think it deeply, the last sentence could not apply: there might be solutions in which several closed tours appears, like:
This is a valid solution given the mathematical definition, so we need a new constraint here. In such constraint, we could add some sort of ordering, considering that we will start and end the closed tour in the same location: Hanoi. I know it’s not so obvious, but if you want (do you?) I can explain it further in a new post, but the new constraint should look like this:
Objective function
In this case we want to minimize the total travel time, so it’s something easy to define in mathematical terms:
If we code this mathematical model and solve it, we would get the following solution…
✍🏻 Some conclusions
So today we’ve seen a translation of a day-to-day thing like making a planning for a trip, but solved with the help of Operations Research.
And then some other questions can arise! What if…
I want to minimize the overall cost of the travel?
I add a lot of locations and let the model tell me which ones I should visit?
I take into account the cost of each transportation system between locations and let the model tell me the best possible option to choose?
Those are just some questions, what are yours?
Let me know in comments if you want me to deep dive into those new issues.
And what’s the best part of a trip? Yes, enjoying it…
Talk soon,
Borja.