#4 📈 Jobs for this technology will grow by 24.6% over this decade
And will most likely continue to do so for decades to come.
In 2013, UPS deployed ORION, an in-house solution that saved it:
38 million liters of gasoline
22,000 tons of CO2
50 million dollars that year
But also:
It delivered 350 000 more packages
Its 55,000 drivers drove 45 million fewer kilometers.
In the years that followed, these figures have been increasing. Especially the one on cost savings. And do you know how it did it?
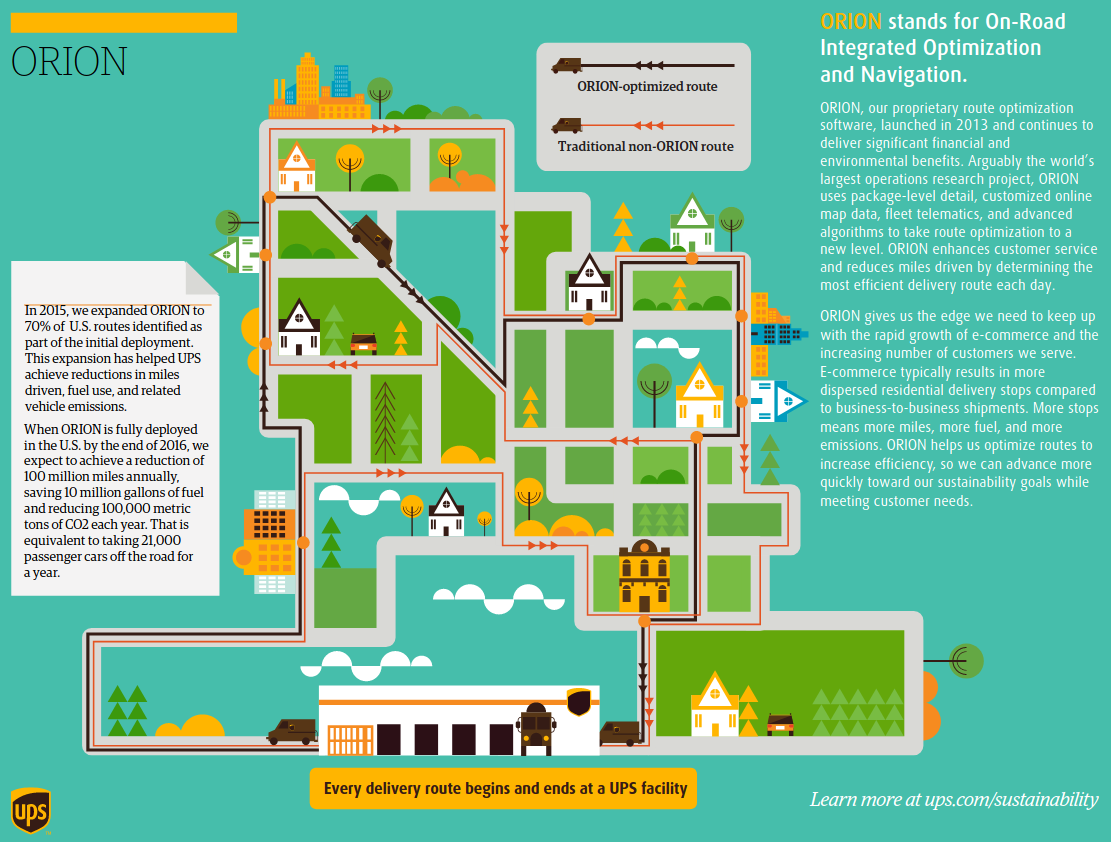
By solving an optimization problem. In fact, ORION is the acronym for On-Road Integrated Optimization and Navigation.
So that's what we're going to look at in today's edition of Feasible:
The knowledge that makes it possible to solve these problems
What is an optimization problem
What you can do about it
Let's go for it!
🤔 The report
According to the US Bureau of Labor Statistics, about 12 million jobs will be created during the decade from 2020 to 2030 in the US.
12 million.
That's about 7.7% year-on-year growth, and several of these jobs are closely related to computer science and mathematics. You can see an excerpt in the image below:
On the vertical axis is the percentage growth in the number of jobs during this decade for different professions. On the horizontal axis would be the average salary, so the further to the right we go, the better salaries we'll find. You can see the full report here. (And I'm lucky enough to work at the intersection of several of those bubbles 😃 but that's another topic we'll cover.)
One of those bubbles has been the great forgotten one for decades. And you'll think "Borja, you're over the top". But no.
It's a bubble that has been here among us since we have computers and can compute faster than doing calculations by hand. Roughly since World War II. In times of scarcity, when there are many constraints and hundreds of thousands of items and people need to be managed and supplied, "a scientific method was born to provide executive departments with a quantitative basis for making decisions about the operations under their control."
Maybe you've already guessed which bubble I'm referring to: the Operations Research Analyst bubble.
And the fact is that it is Operations Research that makes it possible to solve the kind of problems that arise in any business, those of optimization. You remember UPS and its optimization problem, don't you? I haven't really told you about it, but it's the problem of managing tens of thousands of drivers to transport packages at the lowest possible cost.
🎯 Ok, but what is an optimization problem?
You're probably not UPS, a mega-company listed on the New York Stock Exchange, with more than 400,000 employees worldwide and generating profits of $10 billion a year.
But one thing I know for sure: you want to minimize costs, or maximize profits, or drive fewer miles to deliver packages... And all within the constraints of your business: you have the employees you have, the budget you have, the vehicles you have. And you are also trying to allocate resources manually, but you know that as certain variables grow, the problem becomes more and more complex and you sense that the process can be improved.
So that's an optimization problem. Specifically, a combinatorial optimization problem.
The UPS problem is a combinatorial optimization problem. It is a rather complex version of the well-known Traveling Salesman Problem (TSP). In the TSP we have a set of points, which will be the cities to visit, and the objective is to join all those points in such a way that the total distance between them is minimized without passing twice through the same point, making a cycle between all of them.
This, which seems easy at first glance, is not as soon as we increase the number of cities to visit.
Let's do the math:
If we only have 2 cities → 1 possible solution (because traveling one way or the other way is exactly the same, there is actually no cycle here).
If we have 3 cities → 1 possible solution as well. Because A → B → C is exactly the same as B → C → A or as C → A → A → B.
4 cities → 3 possible solutions:
A → B → C → D → A
A → B → D → C → A
A → C → B → D → A
5 cities → 12 possible solutions:
A → B → C → D → E
A → B → C → E → D
A → B → D → C → E
A → B → D → E → C
A → B → E → C → D
A → B → E → D → C
A → C → B → D → E
A → C → B → E → D
A → C → D → B → E
A → C → E → B → D
A → D → B → C → E
A → D → C → B → E
And I'm not going to list more solutions, but....
For 6 cities → 60 possible solutions.
For 7 cities → 360 possible solutions.
For 10 cities → 181 440 possible solutions.
For 15 cities → 653 837 184 000 possible solutions.
For 20 cities → 6.08225502×10¹⁶ possible solutions, or what is the same, a 6 with 16 zeros behind 😮.
You see where this is going, don't you? We add a single city, from 6 to 7, and we go from 60 to 360 solutions to the problem. From 7 to 10 and we go from a few hundred to hundreds of thousands of solutions. And with just 5 more cities we go to hundreds of billions of solutions. The growth in the number of solutions as we increase the number of cities is exponential. Being n the number of cities, for this problem we have a number of solutions equal to:
(n-1)! / 2
And this is something that happens not only for this problem, but in fact for virtually any optimization problem that appears in real life. By increasing the size of the input a little, the output increases exponentially.
❓ What you can do about it
First, identify the problem.
Second, want to solve it in an analytical way.
Third, get to work on it.
UPS did it very well at the time. It had completely identified the problem, wanted to solve it analytically and got on with it. In fact, it took several years to get their project off the ground.
The first step is relatively straightforward, because if you have a business and you care about it, you can identify the problems that appear. The normal thing is that you are even solving the problem by hand or with some excel table or with a very specific knowledge of one or several people. But that doesn't scale.
If you really want to analytically solve such a problem, you need to have people on your staff with knowledge about solving such problems. This is where the role of the Operations Research Analyst comes in. This type of profile is usually found among:
Mathematicians
Industrial engineers
Computer scientists
Masters in Statistics and Operations Research
PhD in Operations Research
And they usually have knowledge in several disciplines, such as:
Statistics
Programming
Mathematical modeling (i.e., the "translation" of business requirements into a mathematical model that describes the reality of the problem)
Algorithms
In future issues of the newsletter I will introduce you to problems that arise in different businesses, such as warehousing, investments, telecommunications or personnel planning.
But in the meantime I leave you with the UPS video in which they talk about their ORION system in more detail:
See you soon.
In the previous edition I used Dall-E from OpenAI to generate the image. Every day more and more AIs are appearing that are able to generate an image according to a given text. And it is not only that more and more AIs are appearing, but they do it tremendously well.