📈 #28 Who is an influencer... According to Graph Theory?
Myths and truths about the number of followers.
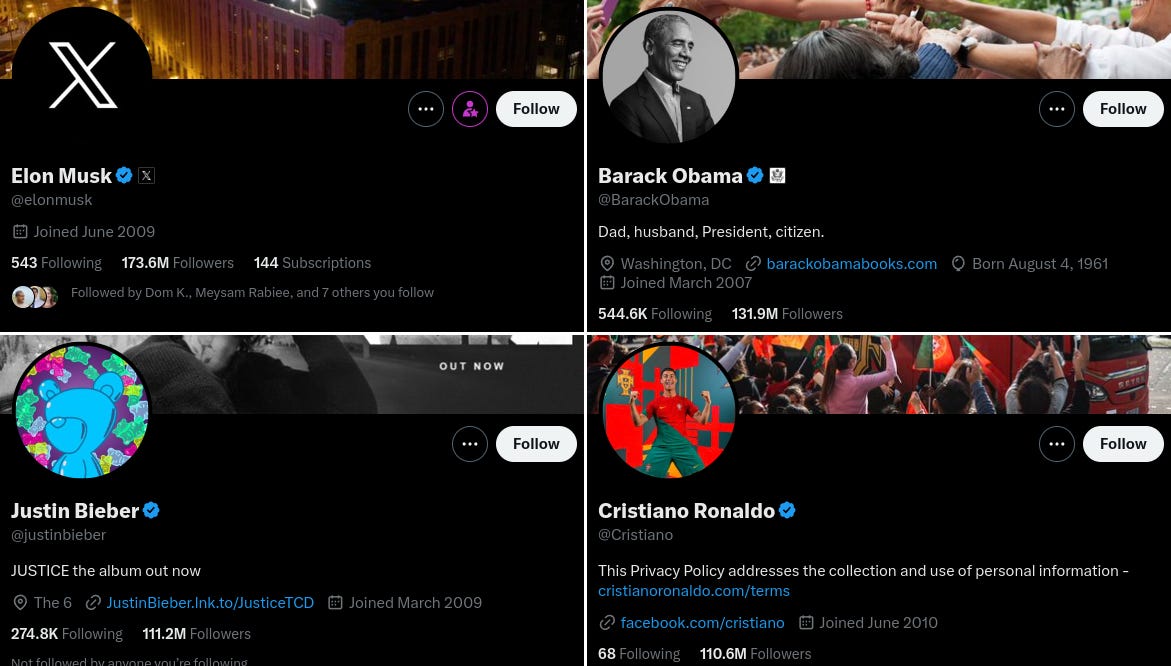
What do the Twitter accounts of Cristiano Ronaldo, Justin Bieber, Barack Obama, and Elon Musk have in common?
Exactly: they are the 4 Twitter accounts with the most followers. More than 100 million each.
When I saw those numbers, the first thing I thought was, "Wow, will I ever reach that number of followers?"
Well, there's practically no chance of that happening.
But the next thing I thought was, "Could I write a tweet that would get more likes than theirs?"
And that's where I saw a possibility. I don't know if it's very high or very low, but it's there.
Because I started to investigate.
Interestingly, neither Cristiano nor Justin Bieber have tweets with half a million likes. They're not even in the top 20 most-liked. However, among tweets with so many likes, I did see one with almost 3 million likes.
One from someone you might not expect.
One from an account that doesn't even have a million followers.
One from...
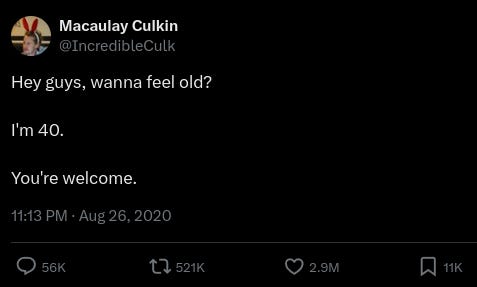
Indeed, Macaulay Culkin.
I don't know if he was home alone or not when he wrote the tweet, but this one from August 2020 earned him almost 3 million likes:
We tend to think that influencers are those with the most followers, but it's clear that's not always the case.
So, the next thing that came to my mind were many questions. Is the number of followers the only thing that matters on a social network to go viral? Is it the way information is distributed? Are algorithms managing everything?
Today, on Feasible, I'll tell you how Operations Research answers these questions through graph theory:
What a social network is
How we can consider someone an influencer according to this theory
How businesses are deeply infused with this theory (even if they don't know it)
Let's go for it!
🕸️ Social networks as graphs
A social network like Twitter primarily has two things:
Users
Relationships between them
And not just Twitter, of course. Also LinkedIn, Instagram, Facebook, or TikTok.
That's why every social network can be defined as a graph: the graph's nodes would be the users that make it up, while the edges would be the existing relationships between the nodes. Graphically, we can see it like this:
Depending on whether the relationships between users are symmetric or not, the relationships are drawn with lines or arrows, respectively.
In a social network with symmetric relationships, it happens that users always follow each other mutually, as in Facebook or WhatsApp. This is known as an undirected graph, and the relationships between users are drawn with lines.
On the other hand, in a social network with asymmetric relationships, users do not necessarily have to follow each other, as happens on Twitter or Instagram. In this case, the graph is directed, and the relationships between users are drawn with arrows indicating who follows whom.
This, which might seem trivial, is the basis for how messages are distributed in the network. Depending on the relationships among its members, who launches the message, or how it's positioned within the network, messages will spread faster or slower.
And it's precisely this message distribution mechanism that leads to the next concept: virality and, more importantly, the influence of certain network nodes (or social network users) for a message to be distributed and receive many visits and likes.
📸 Influencers from graph theory
The influencers of a social network are like the most popular kids in school, those people everyone wanted to be with. Important people.
As such, within the social network, they are also important. In fact, they will be the most important nodes of the network.
But we've seen a bit further up accounts with hundreds of millions of followers that don't have many likes. Moreover, you won't see them in the Top 20, when others, with less than 1 million followers, are there.
So, how can we define the importance of a network node?
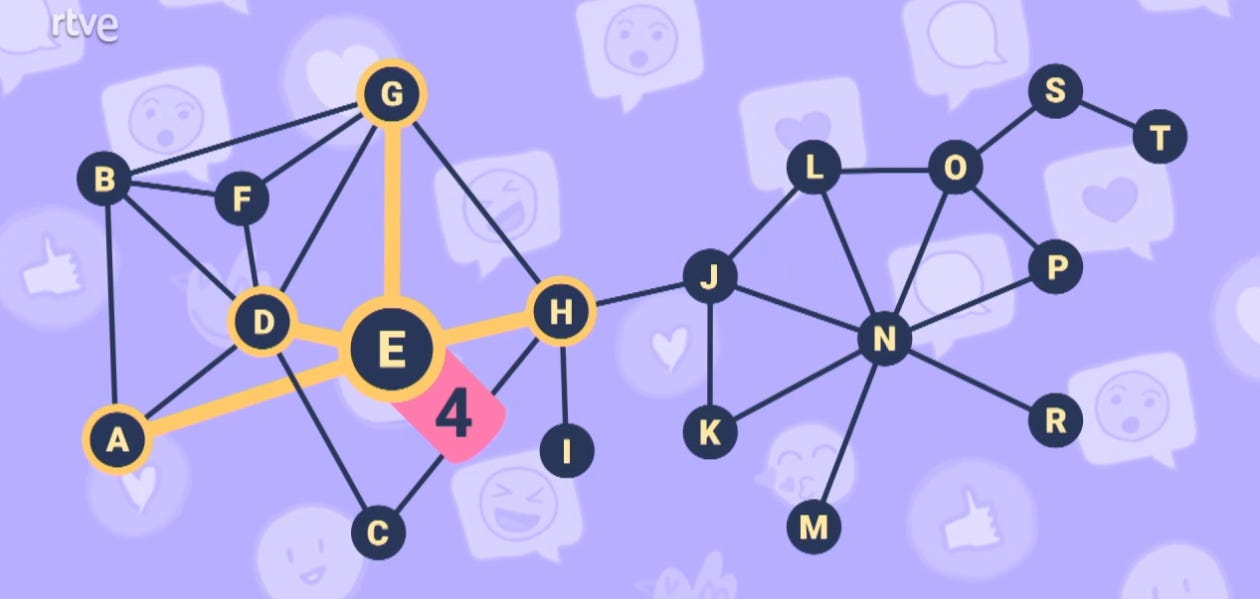
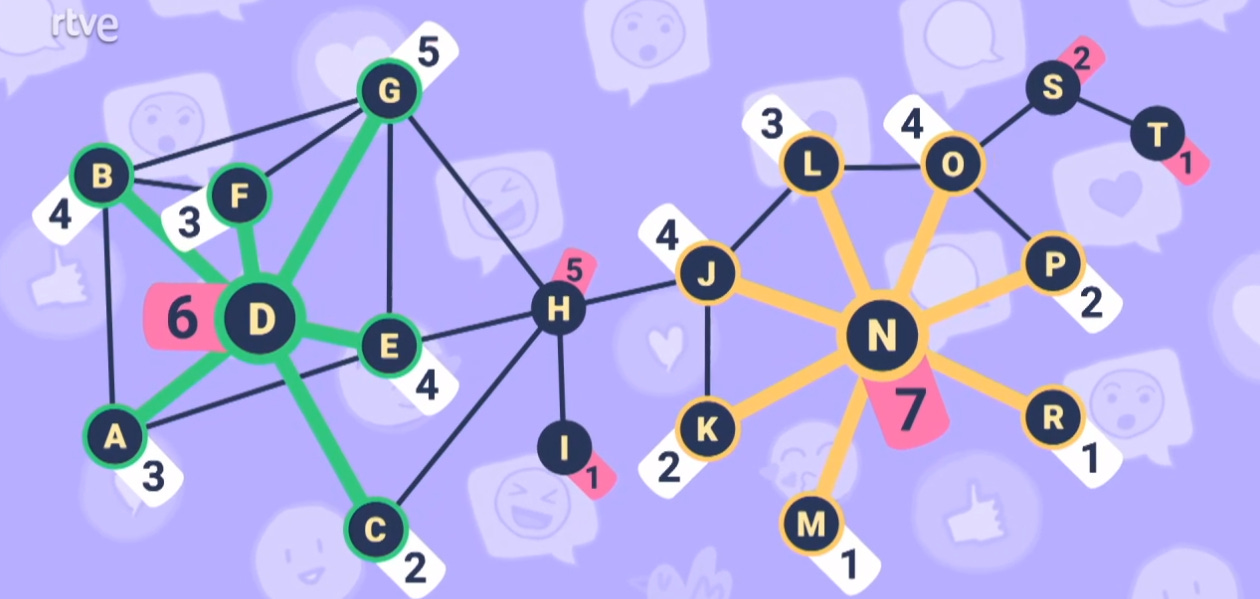
One of the basic concepts in graph theory is the degree of a node, which is nothing more than the number of connections the node has. For example, node E would have a degree of 4 in this graph because it has connections with 4 adjacent nodes (A, D, G, and H):
With this, we can now calculate the degree of any network node and start to determine the importance of each node:
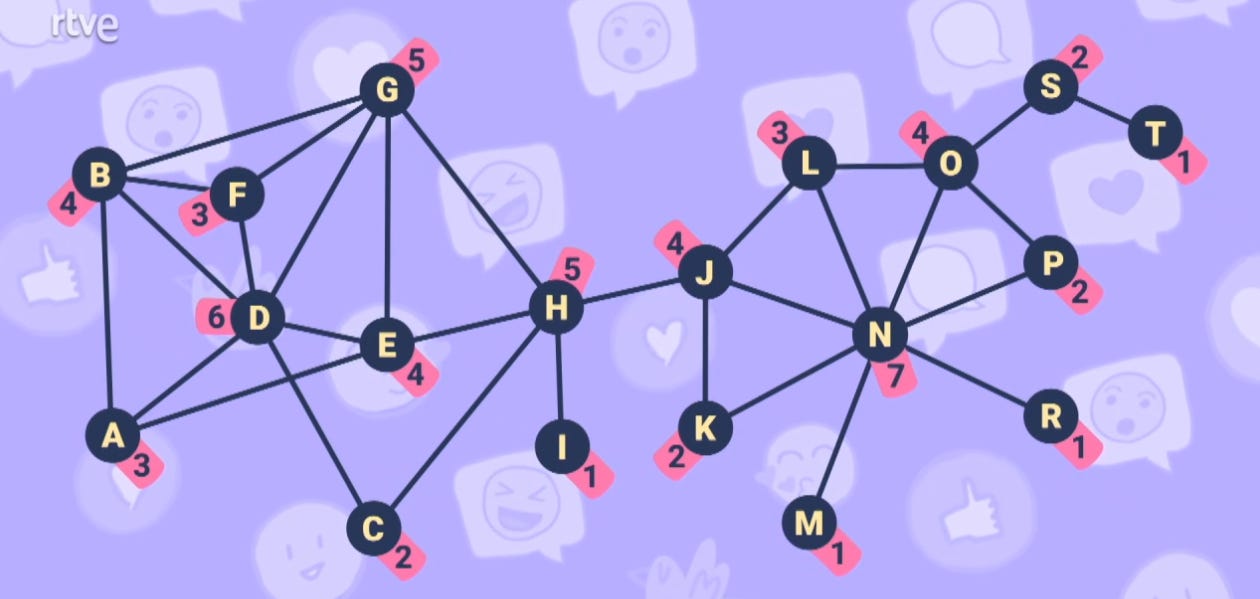
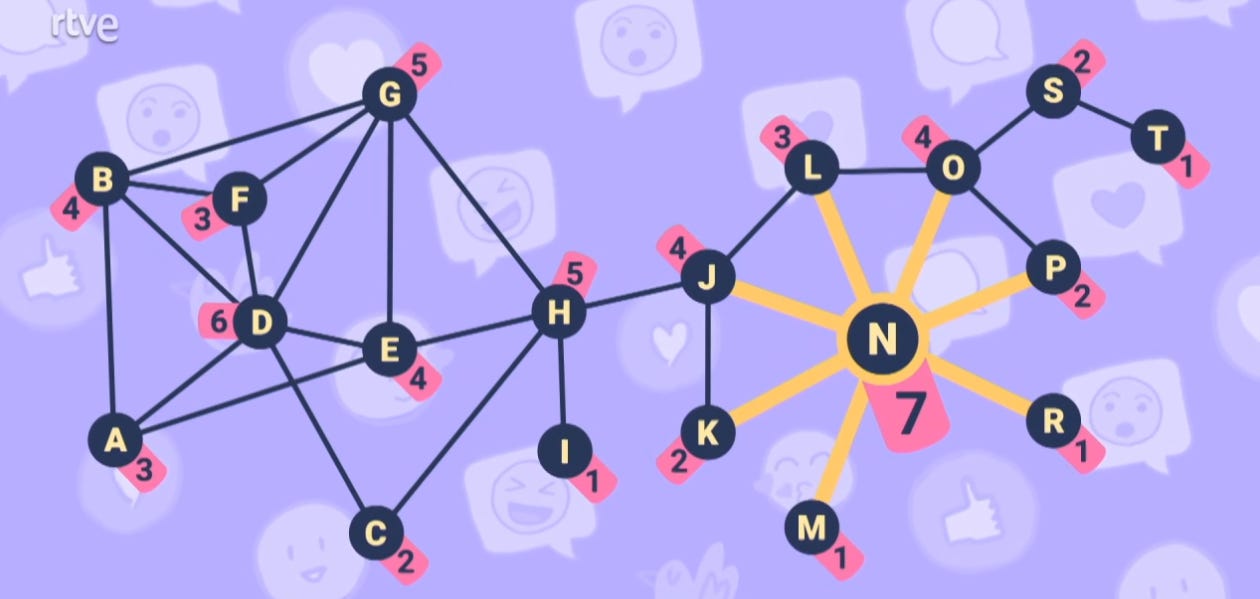
A first proposal to identify the most influential node would be to choose the one with the highest degree, right? Because it's the node that has the most direct contacts. In this case, node N has the highest degree in the entire network:
Would node N be the most important in the network? Maybe not... What's more important: having many contacts, or that your contacts have many contacts in turn? The potential to reach more people is greater in the latter case. And so, the best node for this wouldn't be N but D: the sum of the degrees of its contacts is 21, while the sum of the degrees of the contacts of node N is 17:
Thus, the messages sent by node D would potentially spread more easily through the network than those sent by node N, despite having more direct contacts.
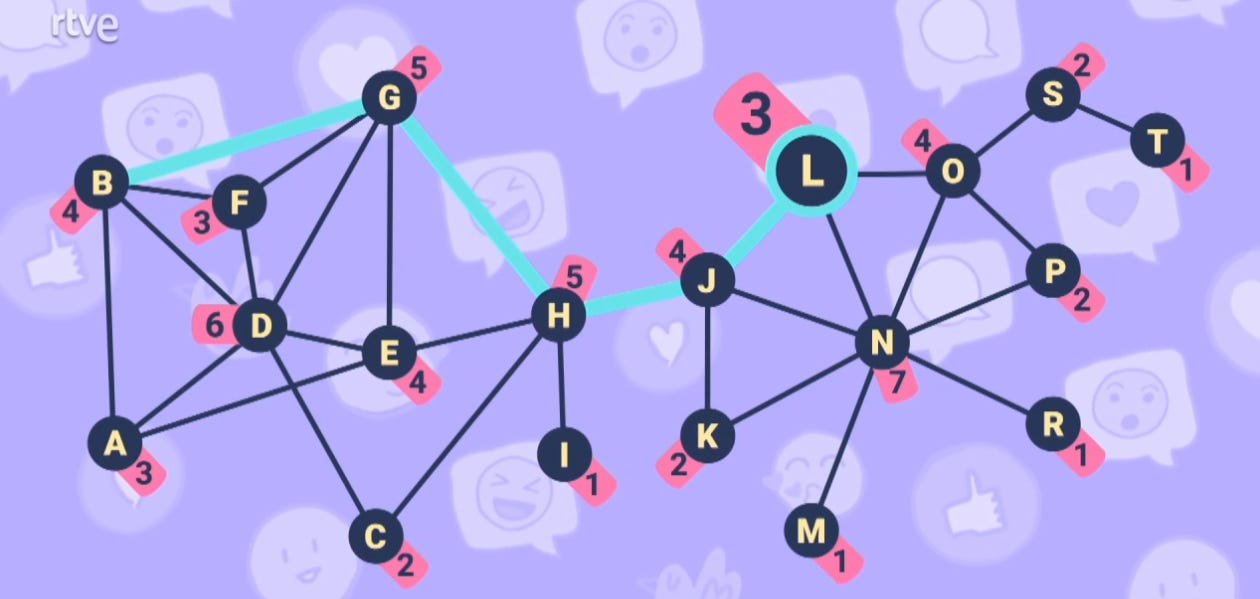
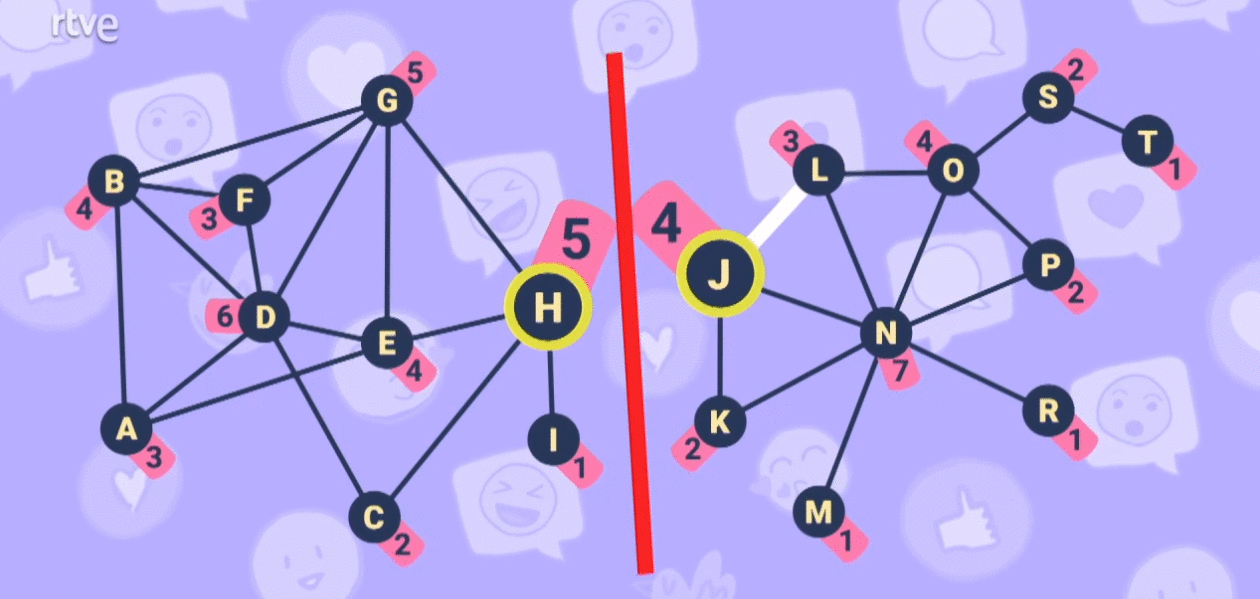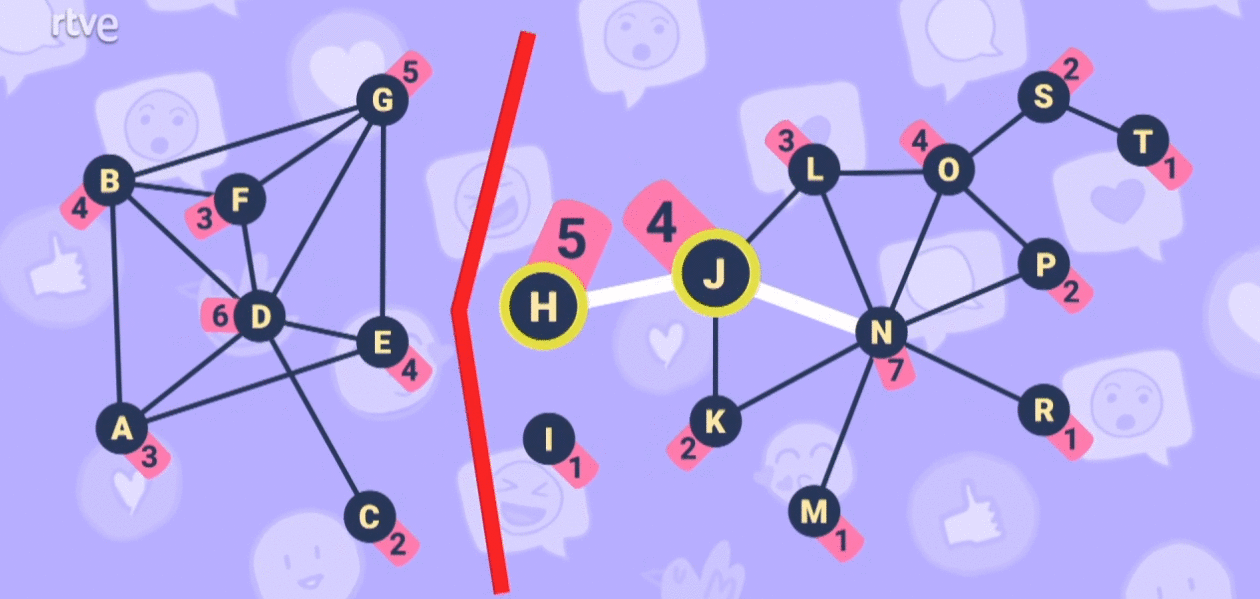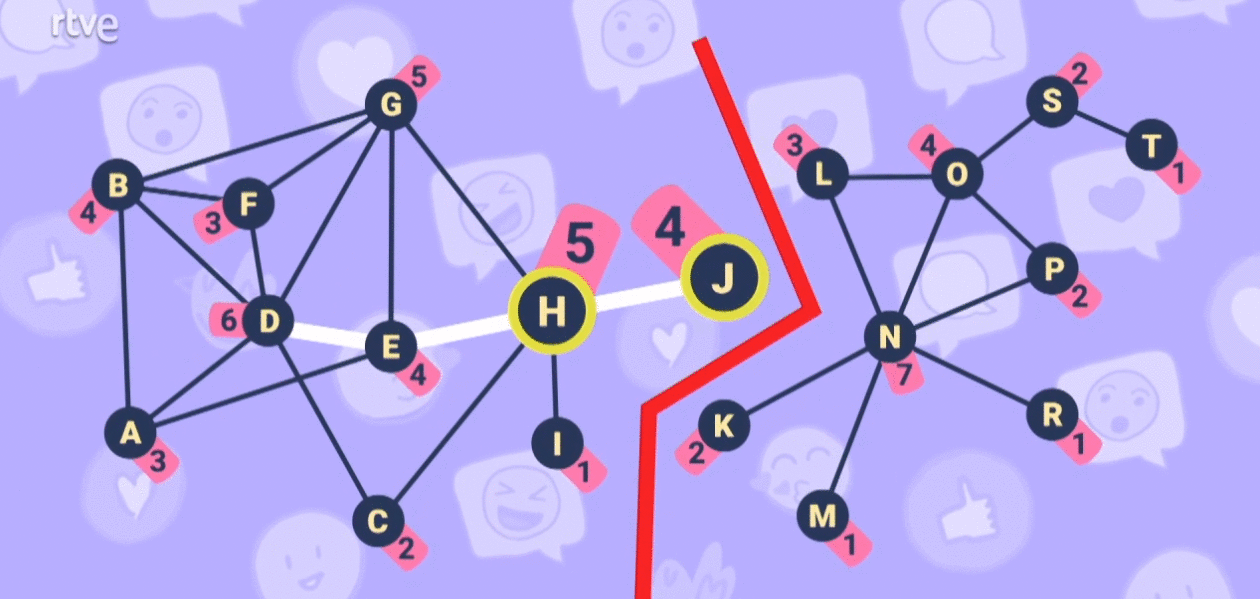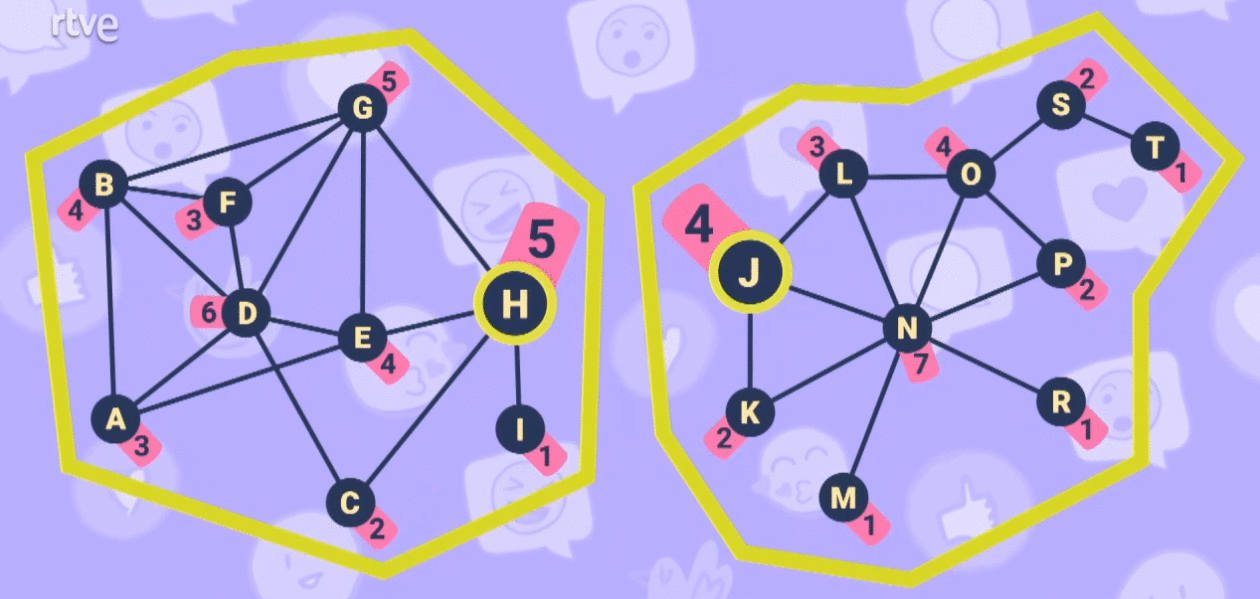
However, I look at the graph and see a serious problem with node D: if it wants to send a message to node T, it takes 7 jumps to get there.
On the other hand, it only takes node L 3 jumps, and to reach the farthest node in the network for it, B, it takes 4 jumps. That is, node L is better positioned if we want to minimize the number of jumps a message has to make through the network:
So, the propagation of a message seems faster if it's done from node L than if it's done from node D.
I don't know if you've noticed, but by the way the graph is shaped, there are specifically two nodes that seem important.
Take another look at any of the previous images.
You see it, don't you?
Nodes H and J might have something to say in all this. If they don't share messages between themselves, those messages don't reach the other side of the network. They are nodes that connect different communities, so they have a great weight within the graph:
So, I'll return the question to you: who would you say now is an influencer within a social network?
💼 Graph theory in business problems
As you can see, graph theory is super useful when analyzing social networks.
And we've only scratched the surface.
The best part about graph theory is that it can be used in a multitude of problems. Think about it, there are many situations that can be defined as a network of nodes connected to each other.
Here are 3 specific examples where it's used.
Route Optimization
In the traveling salesman problem (yes, the TSP we've seen on occasion), we can define the cities as nodes and the paths to go from one city to another as the connections between those nodes.
If we add a weight to each connection, like the distance or the time it takes to go from one city to another... We have our graph.
What we want afterward is to use an optimization algorithm to find the shortest route, and there we can use Dijkstra's algorithm, for example.
Fraud Detection
Financial institutions use graph theory to detect fraudulent transactions.
They model the transaction network, with accounts as nodes and transactions as edges.
Graph algorithms can identify suspicious patterns, such as groups of accounts with unusual activity or sudden spikes in transactions.
By analyzing these connections, they can detect fraudulent activity and prevent financial losses.
Resource Allocation and Planning
Efficient resource allocation and task planning are critical in certain industries like construction or manufacturing. Companies seek to optimize the use of resources such as machinery or personnel while meeting project deadlines and minimizing costs.
In this case, we could treat the tasks or events of a project as the graph's nodes, while the edges would represent the dependencies between them.
Using techniques like the Critical Path Method (CPM), one can identify the longest sequence of tasks that determines the minimum completion time of the project.
By focusing on optimizing the critical path, companies can allocate resources more efficiently, speed up project completion, and reduce costs associated with delays.
These are just 3 examples, but there are many more. An interesting option if you want to delve deeper into graph theory is the Journal of Graph Theory, where there are many interesting open-access articles.
And if you want to dabble in something practical, a Python library with many functionalities is NetworkX. It has very good documentation and is perfect for learning and applying graph theory concepts, and even solving optimization problems with some of its modules.
🏁 Some conclusions
I don't know if Cristiano Ronaldo expected this.
From being one of Twitter's influencers to suddenly Macaulay Culkin, with almost 110 million fewer followers, might be more important than him.
Graph theory has taught us several things today, such as:
A social network is a graph that represents relationships between nodes
Within a social network, some nodes are more important than others
There isn't just one way to measure the importance of the most critical nodes
Graphs are a super useful tool for solving business problems
Now, every time you see relationships between different people, projects, or tasks, you'll see a graph there; it will be inevitable.
But if you've already done it on some occasion... What problems have you already solved using graph theory? Why did you decide to do it that way? What algorithms have you used for it? Tell me in the comments!
See you next week,
Borja.
PS: If you want to watch the TV program that inspired me for this post, it's called A Mathematician Comes to See Me and you can find it here. Clara Grima, a mathematician whom I strongly recommend you follow, spoke very well about virality on social networks.