📈 #17 Solving complex problems made simple with metaheuristics

Effortlessly conquer optimization challenges with streamlined strategies

Dec 03, 2023

Honestly, I didn't think we'd get to this topic so soon, but here we are. This week on Feasible, I want to talk to you about metaheuristics:

Advantages
Limitations
2 specific examples

The main reason is that exact algorithms are the most typical when it comes to solving optimization problems, but they have a significant drawback: there is a class of practically interesting problems for which we don't know exact algorithms with reasonable execution times. Even if an algorithm exists to find solutions, it would take too much time to solve them.

And other techniques are needed, of course.

Once you know them, a new world of possibilities opens up when solving optimization problems.

In fact, I myself started right at this point, and it was what got me hooked on the field. But that's another story. Now...

Let's go for it!

Since I started talking about heuristics a few weeks ago until now, almost without realizing it, you have been advancing to more advanced techniques. The path was clear:

Heuristics → Local Search → Metaheuristics

And it makes more sense this way because these last techniques - metaheuristics - build on previous concepts, improving the solutions found with the techniques I have already presented.

But, what is a metaheuristic?

A high-level master procedure that guides and modifies other heuristics to explore solutions beyond simple local optimality.
Fred Glover, Future paths for integer programming and links to artificial intelligence. Computers and Operations Research, 13:533 549, 1986.

Basically, they work by iteratively evolving a solution or a set of solutions until it is considered good enough that further search for other solutions is stopped.

When I talked to you about local search procedures, we saw that local search gets stuck in a local optimum. Well, metaheuristics come to solve that problem: they can move in the solution space to find a better solution. And they do it thanks to a key concept.

I'm sure you've heard of exploration vs exploitation, which is often discussed in Artificial Intelligence (especially in Reinforcement Learning)… Well, that's exactly what metaheuristics do. I've always known it as diversification vs intensification, but it's exactly the same concept:

Diversification: the idea of moving in the solution space to find different solutions.
Intensification: the idea of intensively exploring a specific area of the solution space to find a local optimum.

So, here are their advantages, limitations, and a couple of metaheuristics.

🚀 Advantages

Metaheuristics have two main advantages over other heuristics/local searches, but also over exact algorithms. They are like the ideal intersection between Local Search and Exact Algorithms.

🔝 They can provide high-quality solutions…

With a metaheuristic, you'll be able to escape from a local optimum, move through the solution space - diversification - and find a better solution - intensification.

Depending on the metaheuristic, it will tend more towards deterministic processes -allowing you to intensify- or stochastic processes -allowing you to diversify.

Finding the right balance between diversification and intensification is key to finding good solutions to the optimization problem you're facing.

⌛ …in a short execution time

Metaheuristics stand out precisely for efficiently finding this balance between diversification and intensification.

⭐ Additionally, they are especially useful when:

The problem is difficult to express in a mathematical model, making it very, very difficult to solve it more traditionally (with a solver).
A traditional method takes too long to execute due to the complexity of the problem itself, and a solution is needed within a constrained time.

🧩 Limitations

Hey, not everything is a walk in the park. Working with metaheuristics also has its challenges. There are several main challenges you face when solving an optimization problem this way.

🎯 The first is optimality. With a metaheuristic, you don't know if the solution is optimal or not. In problems where this is crucial, I would never advise using a metaheuristic in isolation, although it might make sense combined with exact methods to have a very good starting point for finding the optimal solution.

🤓 On the other hand, to harness the full potential of metaheuristics, you need to have a deep knowledge of the problem. It is at that moment that you can generate efficient solution search strategies. And of course, reaching that specific knowledge means investing a lot of time in development. All of this means that all the acquired knowledge and techniques used to solve your problem may not be useful for other problems.

🔢 Finally, it should be noted that metaheuristics have parameters to configure. Some more, and some less. Some have simpler or more understandable parameters, and others more complicated. Therefore, it is also necessary to search for the parameters that best suit solving your problem. If you are familiar with methods like Grid Search or Random Search, the concept is exactly the same: iterate over values of different parameters until you find the right combination that allows you to minimize execution times and find higher quality solutions.

📸 Examples

There are many metaheuristics. Some are based on improving a single solution, and others are based on populations of solutions. Some are based on local search, and others on combinations of solutions. Some are based on multi-start search, and others on estimates of statistical distributions.

Each one has its strengths and weaknesses, and some will obtain good solutions to your problem while others may not.

Choosing one in particular to solve your problem is very complicated.

That's why the best strategy is to prototype 2-3 different ones and see which works best, and then devote more efforts to those strategies that work best.

So here, I'm going to present 2 very different metaheuristics to you, so you understand their differences and start applying them to your next problem.

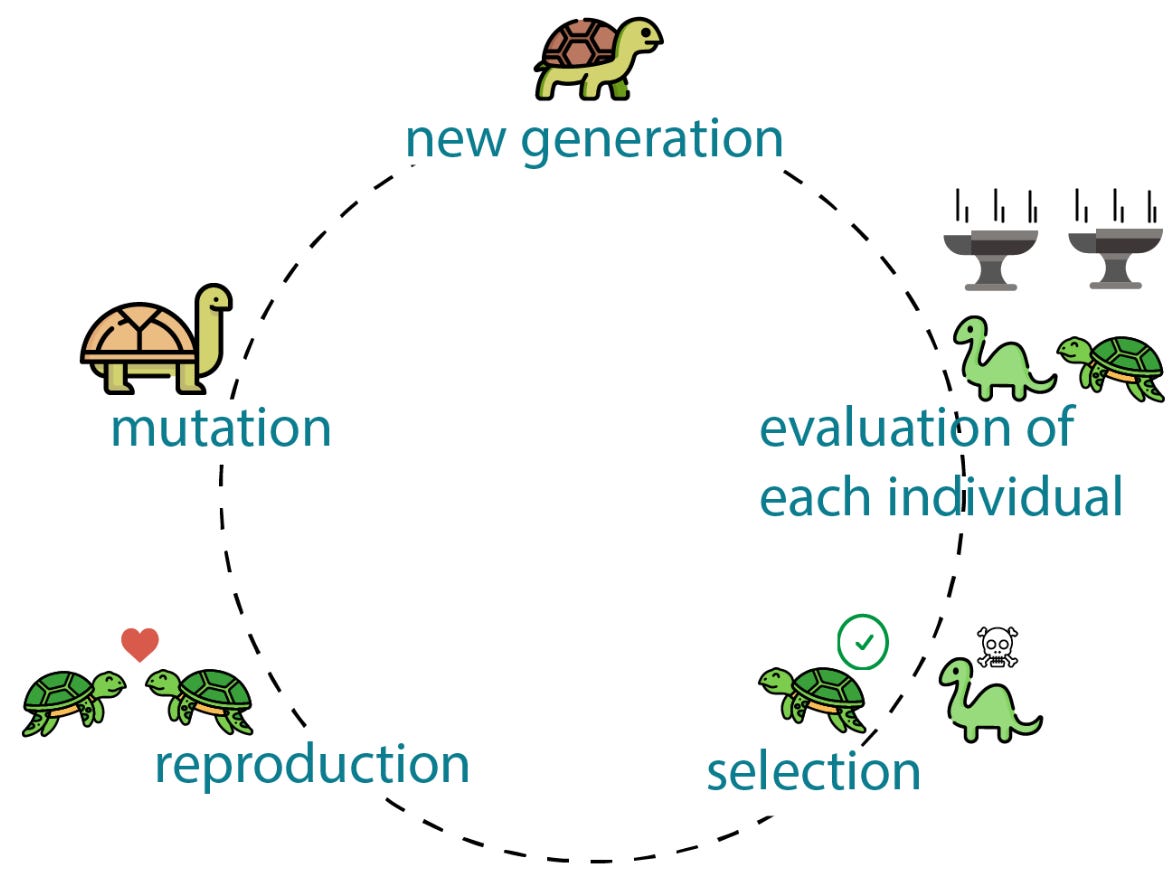
🧬 Genetic Algorithms

These are algorithms based on the neo-Darwinian idea of the evolution of species. They were developed in the mid-1970s by John H. Holland - although more modern versions can be found, like this one - and are inspired by evolutionary algorithms that began their development in the late 1950s. If you were wondering why these algorithms are so famous, now you know one of the reasons, and it's because they are very old.

As the English say: old but gold.

This neo-Darwinian idea of evolution can be expressed as follows:

Individuals that are better adapted to the environment have a higher probability of living longer, so they are more likely to generate offspring that inherit their good characteristics.
In contrast, individuals with poorer adaptation to the environment have a lower probability of survival, so they have fewer opportunities to generate offspring and may eventually become extinct.

From a completely algorithmic point of view, these metaheuristics are:

Population-based, as they operate with a set of solutions called individuals.
Solution combination, as it is typical to choose pairs of individuals - the parents - to combine them and generate a new solution - offspring - that will have good characteristics from those combined solutions. It is also typical to make mutation moves, where an individual changes only a part of itself, mutating.
Evolutionary-inspired, so it is more than evident.

🏘️ Variable Neighborhood Search (VNS)

This is a relatively new metaheuristic, especially compared to genetic algorithms. Here, we find a very different metaheuristic because it is:

Trajectory-based, or in other words, it only operates with a single solution that evolves over time.
Based on local search, as it uses local search methods to intensify and find local optima.
By neighborhoods, as it uses different neighborhood structures to find these optimal solutions.

It is based on three specific points:

A local optimum with respect to one neighborhood does not have to be so with respect to another.
A global optimum is a local optimum with respect to all possible neighborhood structures.
For many problems, local optima with respect to one or several neighborhood structures are relatively close.

The last point, of course, is an empirical observation, but it implies that sometimes a local optimum helps us understand certain information about the global optimum.

I can affirm, and I do affirm, that VNS is my favorite metaheuristic 😍 I have worked a lot with it, doing all kinds of implementations: hybridizing it with other metaheuristics, with multi-start strategies, parallelizing its execution… And it has two very strong points:

It is super flexible
It requires minimal parameterization

I'll tell you more about it in future posts 😉

🏁 Conclusions

It was necessary, but today I've told you so much...

What metaheuristics are
Advantages and limitations they have
2 very famous metaheuristics, one with history and the other with 2 very interesting strong points

But this doesn't end here; this is just the tip of the iceberg! We can delve much deeper and talk about each type of metaheuristic, or talk about parallelization to execute them more quickly, or about their future with hyper-heuristics and mat-heuristics, or even the future of optimization with Reinforcement Learning or Quantum Computing...

Tell me: where do you want me to continue telling you things?

Talk soon,

Borja.